M/M/1 Queuing System
Overview
This example shows how to model a single-queue single-server system with a single traffic source and an infinite storage capacity. In the notation, the M stands for Markovian; M/M/1 means that the system has a Poisson arrival process, an exponential service time distribution, and one server. Queuing theory provides exact theoretical results for some performance measures of an M/M/1 queuing system and this model makes it easy to compare empirical results with the corresponding theoretical results.
Structure
The model includes the components listed below:
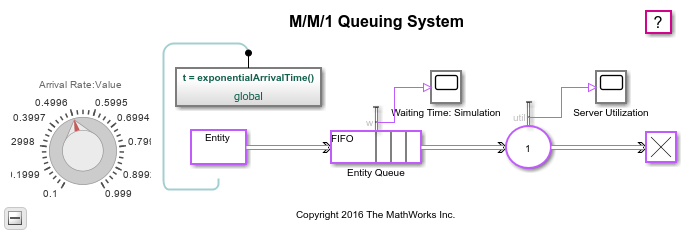
Entity Generator block: Models a Poisson arrival process by generating entities (also known as "customers" in queuing theory).
Simulink Function exponentialArrivalTime(): Returns data representing the interarrival times for the generated entities. The interarrival time of a Poisson arrival process is an exponential random variable.
Entity Queue block: Stores entities that have yet to be served in FIFO order
Entity Server block: Models a server whose service time has an exponential distribution.
Results and Displays
The model includes these visual ways to understand its performance:
Scopes labeled "Waiting Time: Theoretical" and "Waiting Time: Simulation" showing the theoretical and empirical values of the waiting time in the queue, on a single set of axes. You can use this plot to see how the empirical values evolve during the simulation and compare them with the theoretical value.
A scope labeled "Server Utilization" showing the utilization of the single server over the course of the simulation.



Theoretical Results
Queuing theory provides the following theoretical results for an M/M/1 queue with an arrival rate of  and a service rate of
and a service rate of  :
:
Mean waiting time in the queue =

The first term is the mean total waiting time in the combined queue-server system and the second term is the mean service time.
Utilization of the server =

Experimenting with the Model
Move the Arrival Rate knob during the simulation and observe the change in the simulation results
Related Examples
References
[1] Kleinrock, Leonard, Queueing Systems, Volume I: Theory, New York, Wiley, 1975.
See Also
Entity Generator | Entity Server | Queue | Entity Terminator
